25 ++ special right triangles 30 60 90 formula 885964-Special right triangles 30 60 90 calculator

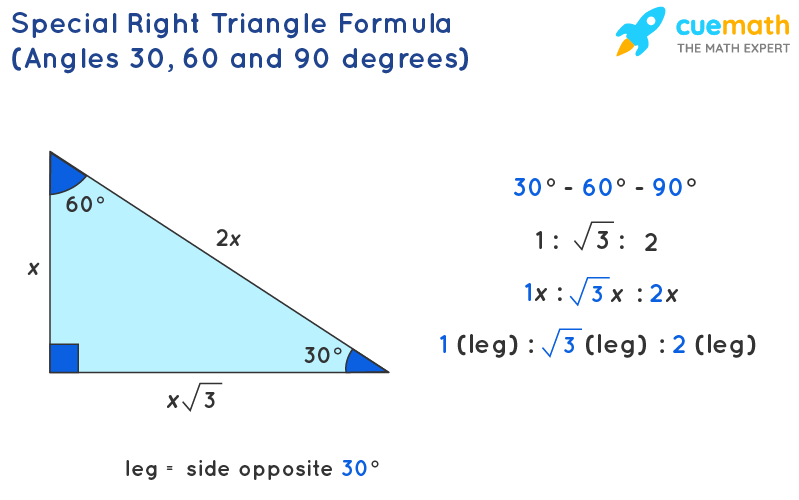
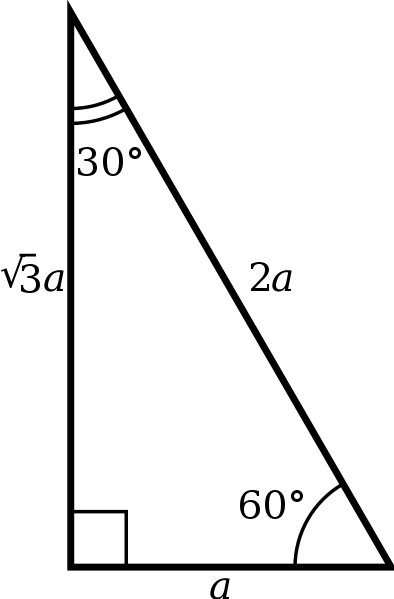
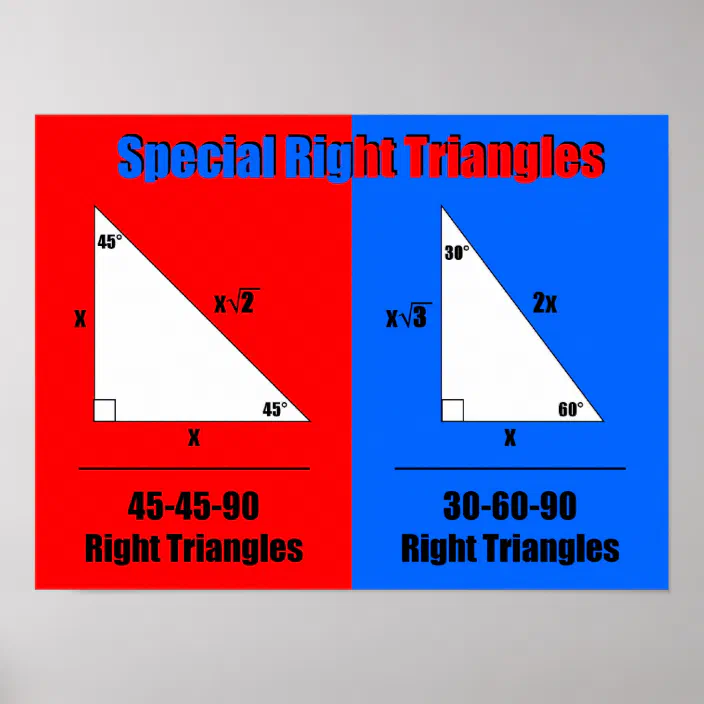
Special Right Triangles inA right triangle (literally pronounced "thirty sixty ninety") is a special type of right triangle where the three angles measure 30 degrees, 60 degrees, and 90 degrees The triangle is significant because the sides exist in an easytoremember ratio 1 √3 3 2 That is to say, the hypotenuse is twice as long as the shorter leg, andA 30̊ 60̊ 90̊ right triangle or rightangled triangle is a triangle with angles 30̊ 60̊ 90̊ Formulas of triangle with angle 30̊ 60̊ 90̊ • perimeter = long side short side hypotenuse;

My College Options Triangles

Special right triangles 30 60 90 calculator

Special right triangles 30 60 90 calculator-Special right triangles 30 60 90 math30 60 90 theorems about special right triangles 45 45 90 and 30 60 90 degree triangles this video discusses two special right triangles how to derive the formulas to find the lengths of the sides of the triangles by knowing the length of one side and then does a few examples using themAlthough all right triangles have special features – trigonometric functions and the Pythagorean theoremThe most frequently studied right triangles, the special right triangles, are the 30, 60, 90 Triangles followed by the 45, 45, 90 triangles

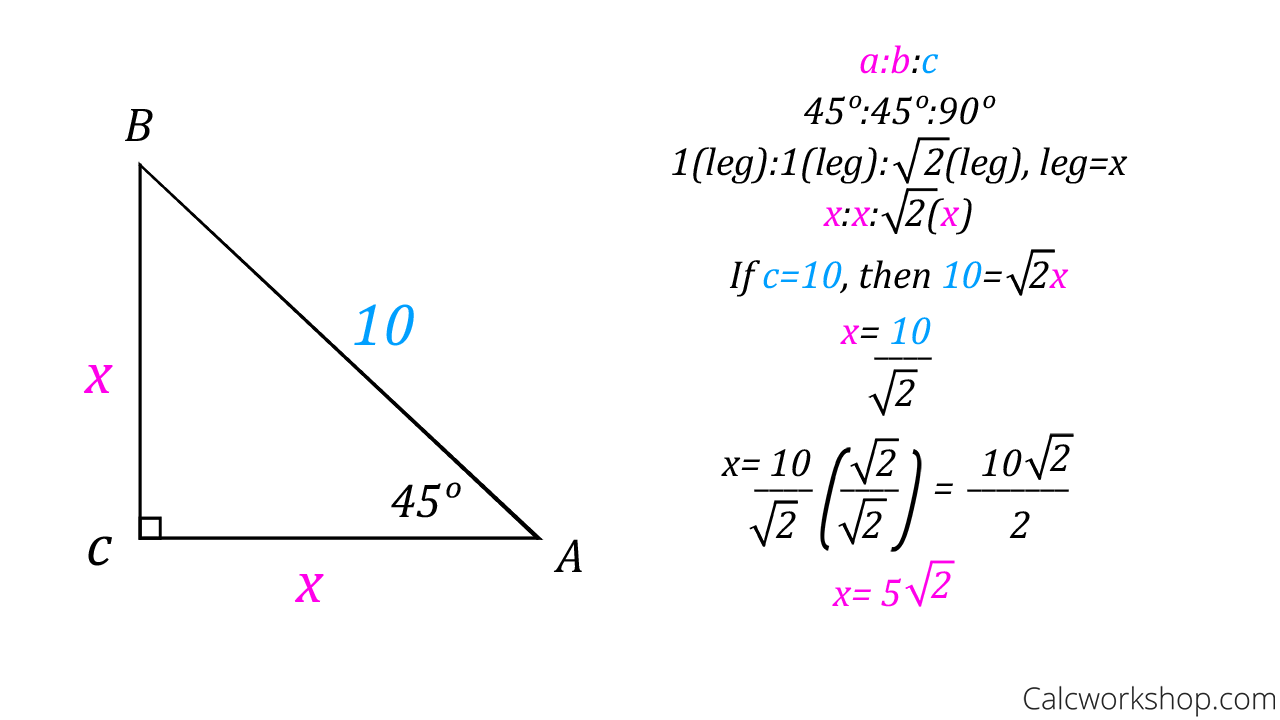
Special Right Triangles Fully Explained W 19 Examples

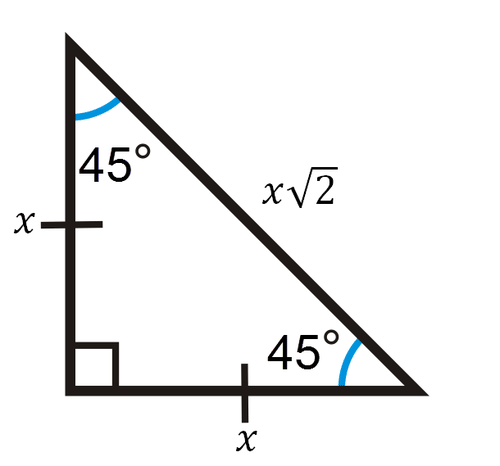
Math 1312 Section 55 Special Right Triangles Note Triangles in this section are always right triangles!A triangle with angle degree measures of 30, 60, and 90 is a special right triangle Corresponding to opposite angle measures, the ratio of the side lengths of every triangle is 1√32 In plain language, the hypotenuse is twice as long as the shortest leg (opposite the 30 degree angle), and the longest leg (opposite the 60 degree angle) is √3 times longer than the shortest legThe Tangent Ratio of Right Triangles;

The Sine Ratio of Right Triangles; The two special right triangles are right triangles with interior angles measuring 30 60 90 and 45 45 90 What is the 45 45 90 triangle rule? A triangle is special because of the relationship of its sides Hopefully, you remember that the hypotenuse in a right triangle is the longest side, which is also directly across from the

As one angle is 90, so this triangle is always a right triangle As explained above that it is a special triangle so it has special values of lengths and angles The basic triangle sides ratio is The side opposite the 30° angle x The side opposite the 60° angle xAbout Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us CreatorsSpecial Triangles Right Triangles FoldableThis foldable explains in an easy way special right triangles theorems Theorem and Theorem Your students will be able to visualize the formulas to find sides lengths of special right triangles and use them to solve problemsThis is a gre

Special Right Triangle Formulas Learn Formulas Related To Special Right Triangles

The Easy Guide To The 30 60 90 Triangle

The other one is the 45 45 90 triangle These triangles are special triangles because the ratio of their sides are known to us so we can make use of this information to help us in right triangle trigonometry problems In the case of the triangle, their side's ratios are 1Triangles Theorem 1 In a triangle whose angles measure 45 0, 45 0, and 90 , the hypotenuse has a length 0 equal to the product of 2 and the length of either leg The ratio of the sides of a triangle are x x x 2Times the square root of three because of the special right triangle rule for 30 60 90 triangles, 1/2 times s over two squared of three times s and multiplying everything out That gives you s squared times the square root of three over four and looking at the formula provided in the problem, you see that it is 1/4 times s squared times the

Right Triangles 45 45 90 Special Right Triangles Notes And Practice

Special Right Triangles Fully Explained W 19 Examples

Specialrighttrianglesworksheetanswers 1/1 Downloaded from optimustestfreenodenet on by guest Read Online Special Right Triangles 30 60 90 Worksheet Answers When people should go to the book stores, search initiation by shop, shelf by shelf, it is in fact problematicTriangle Ratio A degree triangle is a special right triangle, so it's side lengths are always consistent with each other The ratio of the sides follow the triangle ratio 1 2 √3 1 2 3 Short side (opposite the 30 30 degree angle) = x xFile Type PDF Special Right Triangles 30 60 90 Worksheet Answersfact that if α, α δ, α 2δ are the angles in the progression then the sum of the angles 3α 3δ = 180° After dividing by 3, the angle α δ must be 60° Special right triangle Wikipedia Special right triangle 30° 60° 90° is one of the most popular right

Solve A 30 60 90 Triangle With Gradea

My College Options Triangles

 A triangle is a special right triangle (a right triangle being any triangle that contains a 90 degree angle) that always has degree angles of 30 degrees, 60 degrees, and 90 degrees Because it is a special triangle, it also has side length values which are always in a consistent relationship with one another5 rows  Special right triangles 30 60 90 Special right triangle 30° 60° 90° is oneThanks to all of you who support me on Patreon You da real mvps!

Special Triangles Hiset Math

Special Right Triangles Ck 12 Foundation

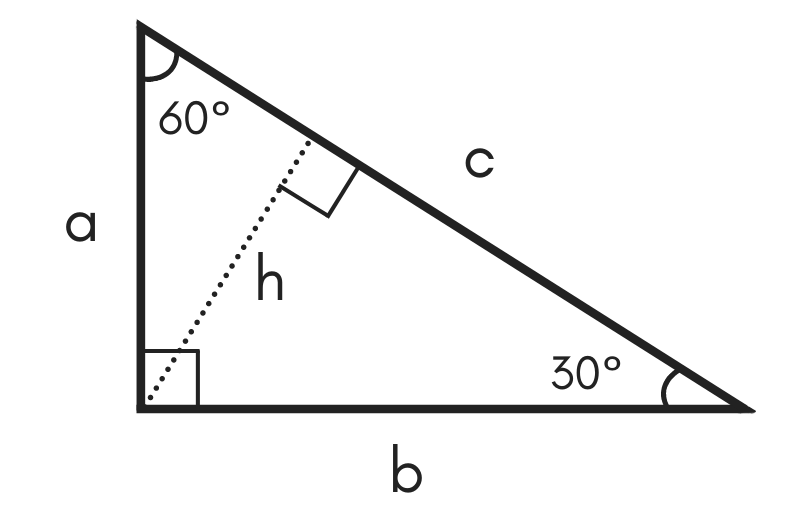
What I want to do in this video is discuss a special class of triangles called triangles and I think you know why they're called this the measures of its angles are 30 degrees 60 degrees and 90 degrees and what we're going to prove in this video this tends to be a very useful result at least for a lot of what you see in a geometry class and then later on in trigonometry class is theStudents also learn that in a 30°60°90° triangle, the length of the long leg is equal to root 3 times the length of the short leg, and the length of the hypotenuse is equal to 2 times the length of the short leg Students are then asked to find the lengths of missing sides of 45°45°90° and 30°60°90° triangles using these formulas 30 60 90 triangle sides If we know the shorter leg length a, we can find out that b = a√3 c = 2a If the longer leg length b is the one parameter given, then a = b√3/3 c = 2b√3/3 For hypotenuse c known, the legs formulas look as follows a = c/2 b = c√3/2 Or simply type your given values and the 30 60 90 triangle calculator will do the rest!

30 60 90 Triangle Definition Theorem Formula Examples

30 60 90 Triangles

Download Ebook Special Right Triangles 30 60 90 Answers fact that if α, α δ, α 2δ are the angles in the progression then the sum of the angles 3α 3δ = 180° After dividing by 3, the angle α δ must be 60° Special right triangle Wikipedia Special right triangle 30° 60° 90° is one of the most popular right triangles Its Page 7/23 A triangle is a special right triangle whose three angles measure 30°, 60° and 90° The ratio of its side lengths (base height hypotenuse) is1 √3 2 Apart from the above two types, there are some other special right trianglesPythagorean theorem special right triangles i can solve for the 2 missing sides of a 30°60°90° assignment 30°60°90° worksheet give answers to fillable 3x5 recipe card template c45 coke cooler This worksheet contains problems on special right triangles

Special Right Triangles Formulas 30 60 90 And 45 45 90 Special Right Triangles Examples Pictures And Practice Problems

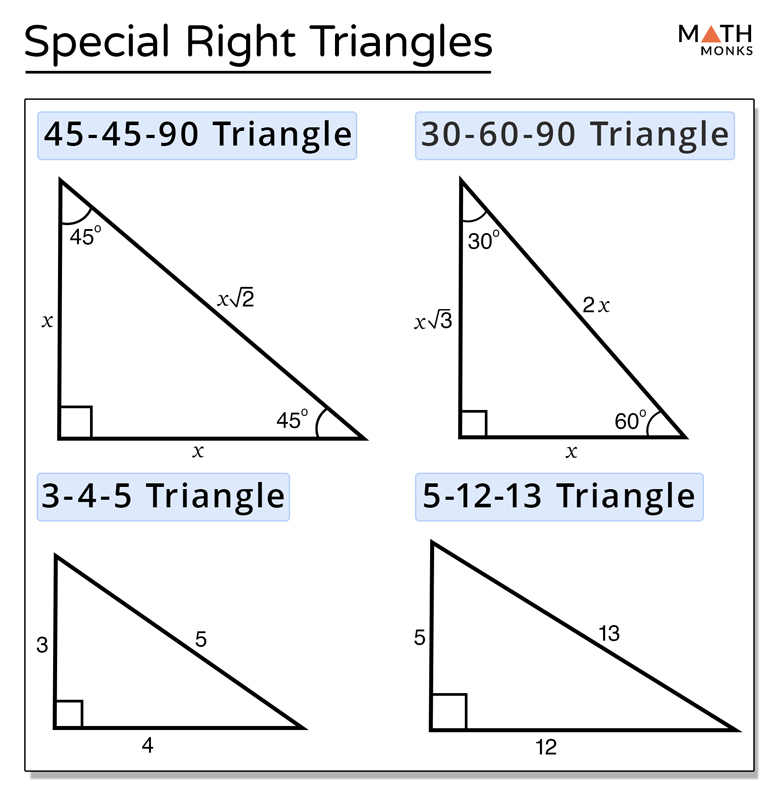
Special Right Triangles Definition Formula Examples

Multiply this answer by the square root of 3 to find the long leg Type 3 You know the long leg (the side across from the 60degree angle) Divide this side by the square root of 3 to find the short side Double that figure to find the hypotenuse Finding the other sides of a triangle when you know the hypotenuseThe 45 45Right Triangles 30 60 90 Special Right Triangles Notes and Practice This packet includes information on teaching 30 60 90 Special Right Triangles I have included *** Teacher Notes with worked out formulas, diagrams and workout examples(the diagram on the first page comes from my set of Right

Learn About The 30 60 90 Triangle Caddell Prep Online

Special Right Triangles 30 60 90 And 45 45 90 Triangles Youtube

Special Right Triangles A special right triangle is one which has sides or angles for which simple formulas exist making calculations easy Of all these special right triangles, the two encountered most often are the 30 60 90 and the 45 45 90 triangles For example, a speed square used by carpenters is a 45 45 90 triangleThe two "special" right triangles are the 30º30º90º right triangle and the 45º45º90º right triangle The 30 º 60 º90 º Right Triangle THE SIDES OF THIS TRIANGLE ARE IN THE RATIO OF 1 TO 2 TO THE SQUARE ROOT OF THREE ( OR IN THIS CASE, X TO 2X TO THE SQUARE ROOT OF THREE TIMES X )Triangles are classified as "special right triangles" They are special because of special relationships among the triangle legs that allow one to easily arrive at the length of the sides with exact answers instead of decimal approximations when using trig functions

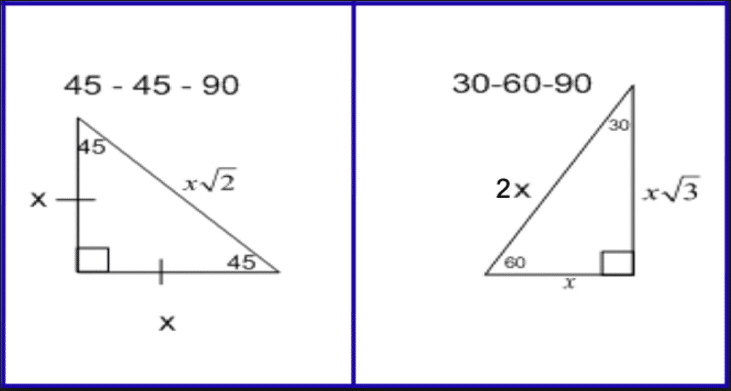
Special Right Triangles Complete Reference Guide The Education

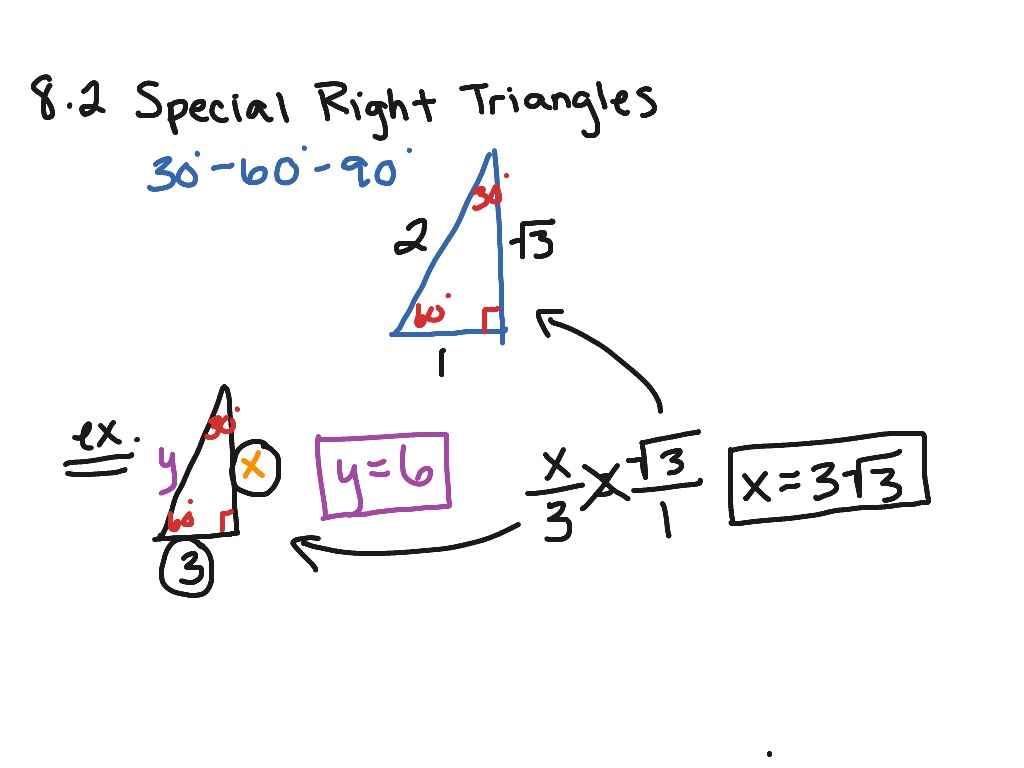
8 2 Special Right Triangles Math Geometry Middle School Math 7th Grade Math 7 G 1 7 G 2 Showme

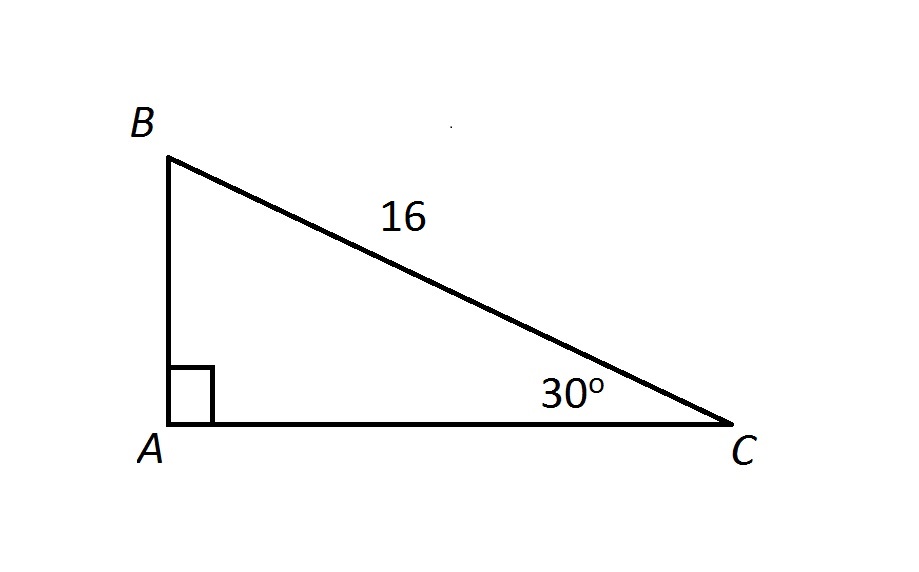
The Cosine Ratio ofOnce the sides of the 30º60º90º triangle are established, a series of relationships (patterns) can be identified between the sides of the triangle ALL 30º60º90º triangles will possess these same patterns These relationships will be referred to as " short cut formulas " that can quickly answer questions regarding side lengths of 30º60º90º triangles, without having to apply any otherSolution To find Length of the sides of the triangle Base = 5√3 (given) Using special right triangles formulas, Base, height, and hypotenuse of a triangle with the angles 30, 60, and 90 degrees are in a ratio of 1√3 2 Let, base = 5√3 = x Then, height = (5√3)√3= 5 *3 = 15 And, hypotenuse = 2x = 2*5√3 = 10√3

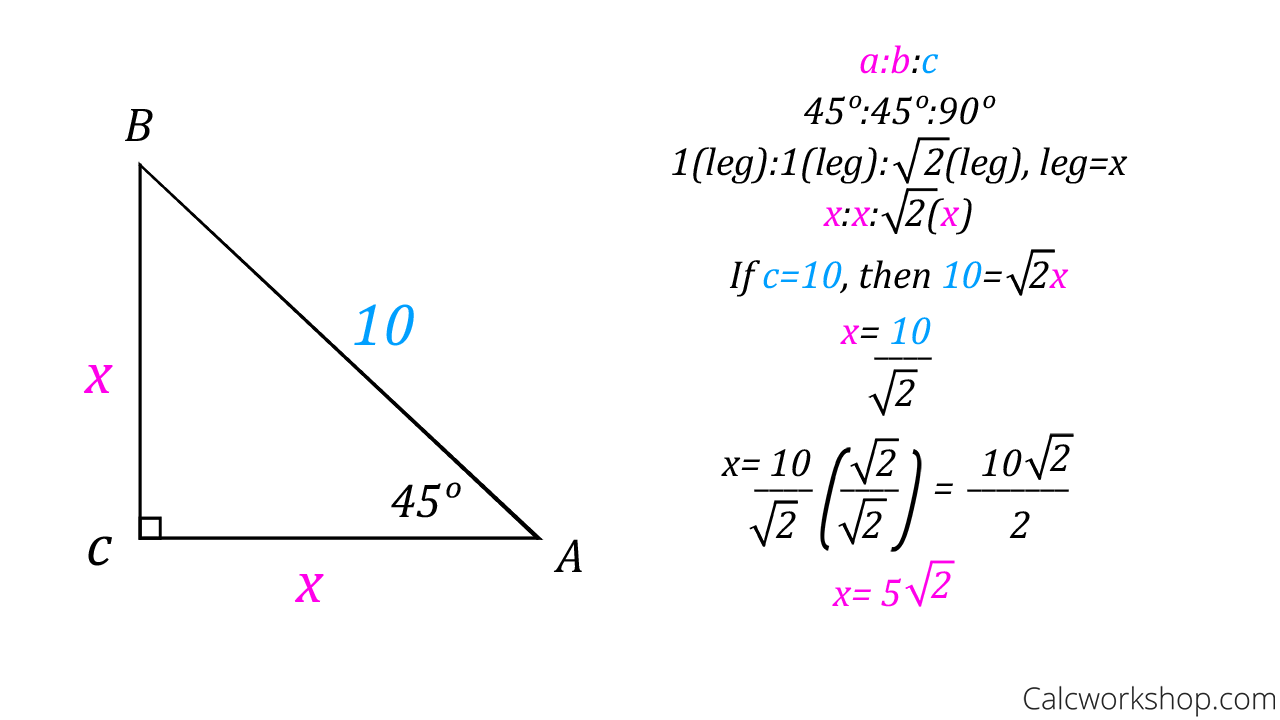
Special Right Triangles Fully Explained W 19 Examples

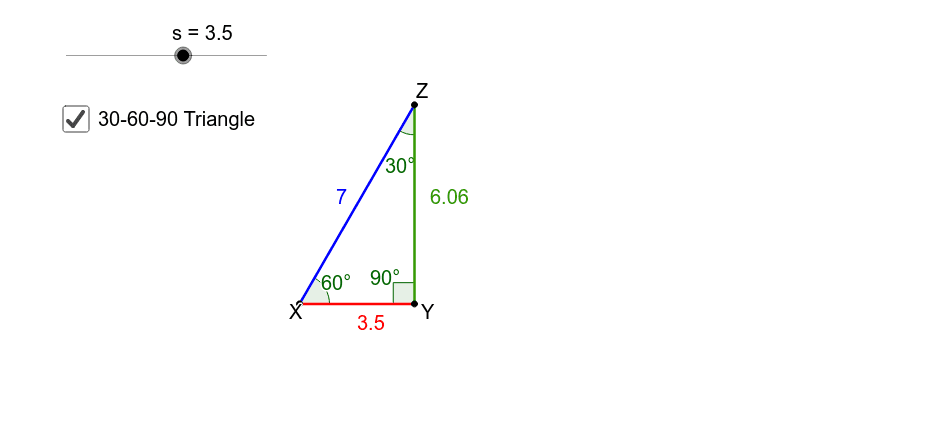
Special Right Triangles 30 60 90 Geogebra

Special Triangles Isosceles and Calculator This calculator performs either of 2 items 1) If you are given a right triangle, the calculator will determine the missing 2 sides Enter the side that is known After this, press Solve Triangle 2) In addition, the calculator will allow you to same as Step 1 with a right triangleSpecial Right Triangles Formulas 30 60 90 and 45 45 90 2 hours ago Mathwarehousecom Visit Site Although all right triangles have special features – trigonometric functions and the Pythagorean theoremThe most frequently studied right triangles, the special right triangles, are the 30, 60, 90 Triangles followed by the 45, 45, 90 triangles See Also Free Catalogs ShowA degree triangle is a special right triangle, so its side lengths are always consistent with each other The ratio of the sides follow the triangle ratio given by the Formula as, 1 √3 2 Thus, for a triangle, the dimensions of the sides can be given as

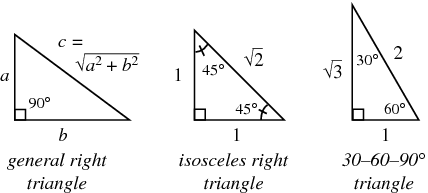
Right Triangle From Wolfram Mathworld

5 8b 30 60 90 Special Right Triangles Youtube

There are two "special" right triangles that will continually appear throughout your study of mathematics the 30º60º90º triangle and the 45º45º90º triangle The special nature of these triangles is their ability to yield exact answers instead of decimal approximations when dealing with trigonometric functions  Right Triangles Hypotenuse equals twice the smallest leg, while the larger leg is sqrt (3) times the smallest % Progress MEMORY METER This indicates how strong in your memory this concept is Practice Preview Assign Practice$1 per month helps!!

Special Right Triangles Interactive Notebook Page Math Methods Teaching Geometry Teaching Math

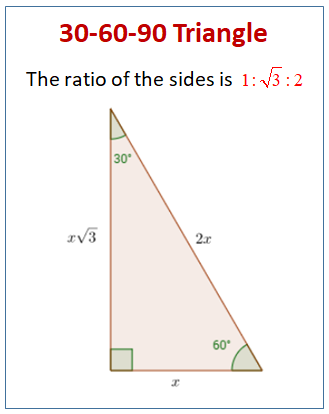
30 60 90 Special Right Triangles Videos Worksheets Examples Solutions

Title Special Right Triangles 30º 60º 90º Author SFSD Last modified by SFSD Created Date PM Company SFSD Other titles tan (60) = √3/1 = 173 The right triangle is special because it is the only right triangle whose angles are a progression of integer multiples of a single angle If angle A is 30 degrees, the angle B = 2A (60 degrees) and angle C = 3A (90 degrees)A special right triangle is a right triangle with some regular feature that makes calculations on the triangle easier, or for which simple formulas exist Angle based right triangle , (Angles that form a simple ratio) Side based right triangle 345 (The lengths of the sides form a whole number ratio), approx angles 3753

Special Right Triangle 30º 60º 90º A Plus Topper

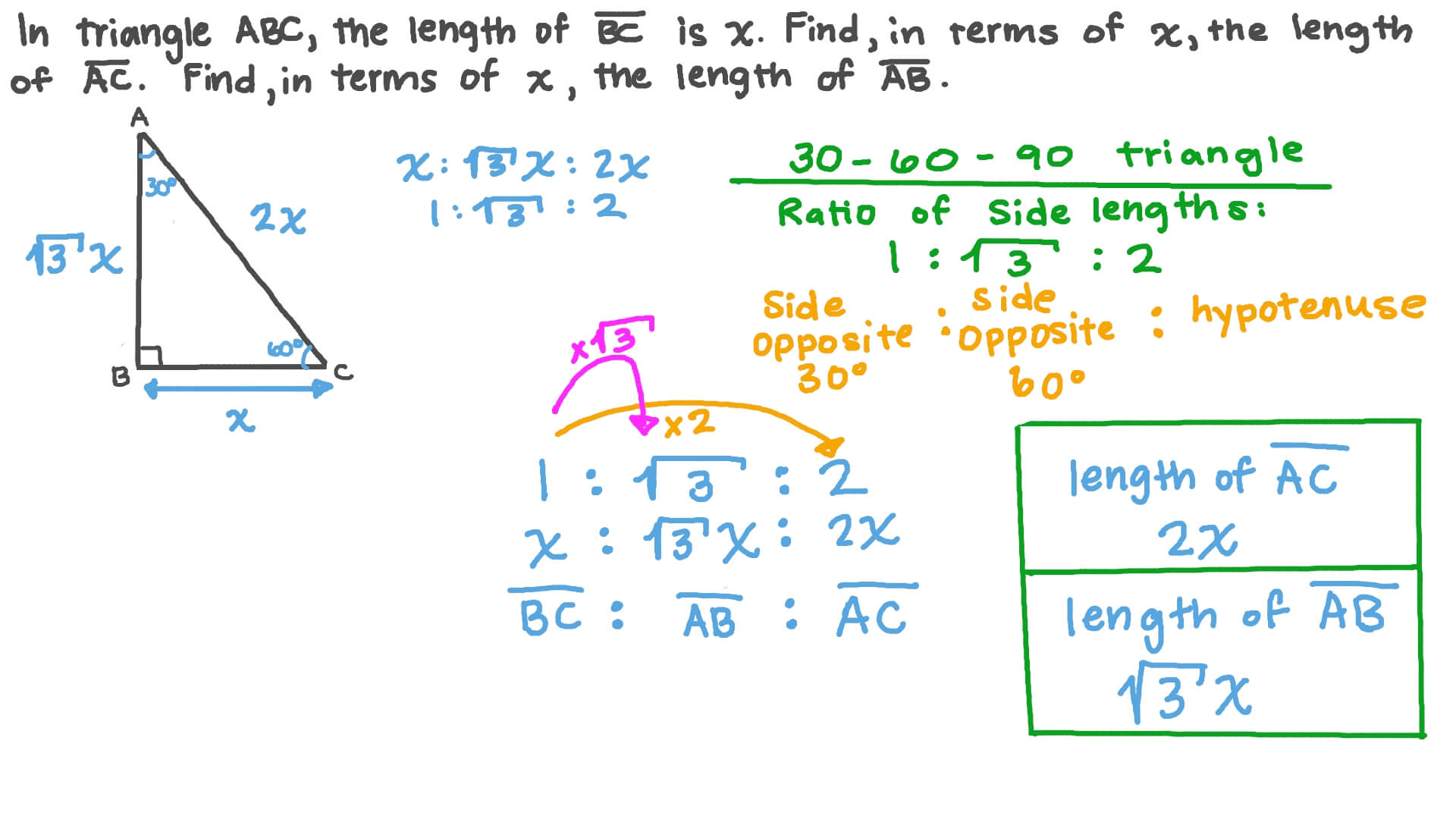
Question Video The Side Lengths Of 30 60 90 Triangles Nagwa

 And so on Đang xem Geometry triangle practice The side opposite the 30° angle is always the smallest, because 30 degrees is the smallest angle The side opposite the 60° angle will be the middle length, because 60 degrees is the midsized degree angle in this triangle And, finally, the side opposite the 90° angle will always be• area = 05 * Because it is a special triangle, it also has side length values which are always in a consistent relationship with one another The basic triangle ratio is Side opposite the 30° angle x Side opposite the 60° angle x * √ 3 Side opposite the 90° angle 2 x

30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com

30 60 90 Triangle Calculator Formula Rules

Right Triangles 30 60 90 Special Right Triangles Notes and Practice This packet includes information on teaching 30 60 90 Special Right Triangles I have included *** Teacher Notes with worked out formulas, diagrams and workout examples(the diagram on the first page comes from my set of Right Triangle Unit Vocabulary Cards and Posters) *** Student Notes so that they canThe Length of a Right Triangle's Altitude (Geometric Mean) The Length of a Right Triangle's Leg (Geometric Mean) Pythagorean Theorem;

45 45 90 And 30 60 90 Triangles Zona Land Education

30 60 90 Triangles Special Right Triangle Trigonometry Youtube

Special Right Triangle Wikipedia

30 60 90 Triangle Formulas Rules And Sides Science Trends

30 60 90 Right Triangles Free Math Help

Right Triangles Gmat Free

A Quick Guide To The 30 60 90 Degree Triangle Dummies

30 60 90 Triangle Explanation Examples

5 30 60 90 Triangles Geometry15a

Special Right Triangles Video Lessons Examples And Solutions

The Converse Of The Pythagorean Theorem And Special Triangles Geometry Right Triangles And Trigonometry Mathplanet

Special Right Triangles Poster Zazzle Com

The Easy Guide To The 30 60 90 Triangle

30 60 90 Triangle Theorem Ratio Formula Video

45 45 90 Special Right Triangle Calculator Inch Calculator

Special Right Triangles Review Article Khan Academy

30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com

30 60 90 Special Right Triangle Calculator Inch Calculator

The Easy Guide To The 30 60 90 Triangle

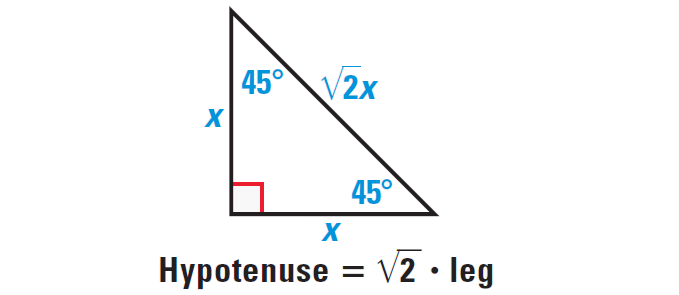
Special Right Triangles

1

Special Right Triangle 30 60 45 45 37 53 Elearning

30 60 90 Right Triangles Read Geometry Ck 12 Foundation

30 60 90 Triangle Theorem Ratio Formula Video

30 60 90 Triangle Sides Examples Angles Full Lesson

30 60 90 Triangle Calculator Formula Rules

30 60 90 Triangle Theorem Ratio Formula Video

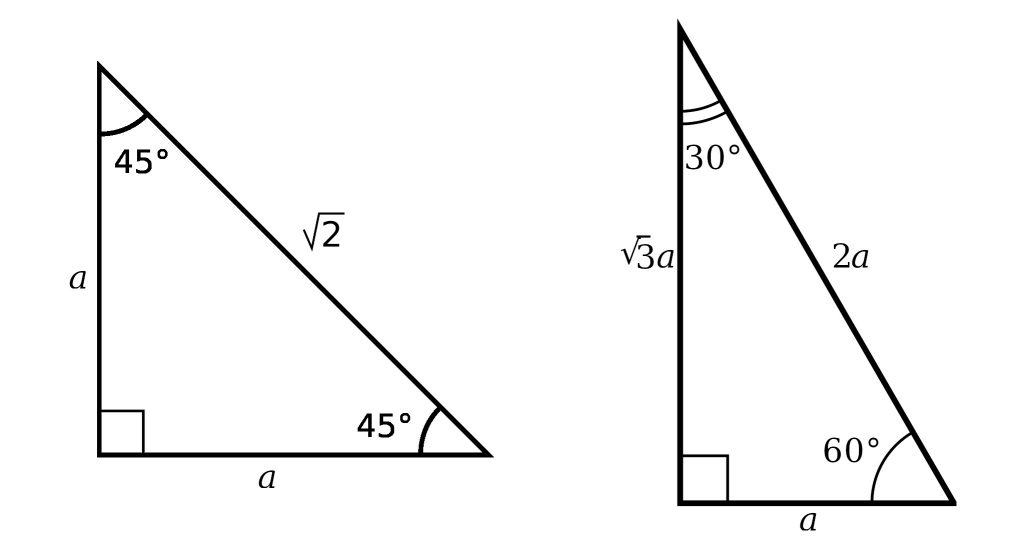
Special Right Triangles Sss a Examples Included

30 60 90 Special Right Triangle Calculator General Knowledge Book Right Triangle Electrical Engineering Books

30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com

Ms Liefland Harper Junior High Geometry 12 3 Through 12 7

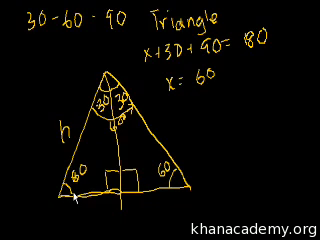
Special Right Triangles Intro Part 2 Video Khan Academy

Special Right Triangles Geometry

30 60 90 Triangles

Act Set 6 Special Right Triangle Rules Flashcards Quizlet

30 60 90 Triangle Theorem Ratio Formula Video

1

How To Work With 30 60 90 Degree Triangles Education Is Around

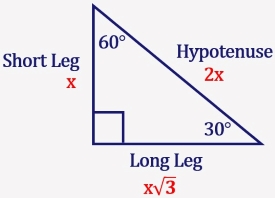
Special Right Triangle 30 60 90 Mathondemand Com

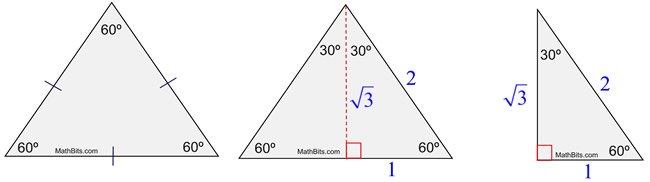
Special Right Triangle 30 60 90 Mathbitsnotebook Geo Ccss Math

Special Right Triangles

Special Right Triangles 45 45 90 Amp 30 60 90 Formula Finding Missing Side Lengths Brainly Com

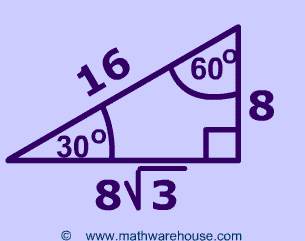
Special Right Triangles Formulas 30 60 90 And 45 45 90 Special Right Triangles Examples Pictures And Practice Problems

30 60 90 Triangle Calculator Formula Rules

Conquering Right Triangles The Pythagorean Theorem On Act Math Part 1 Magoosh Blog High School

Right Triangles 30 60 90 Special Right Triangles Notes And Practice

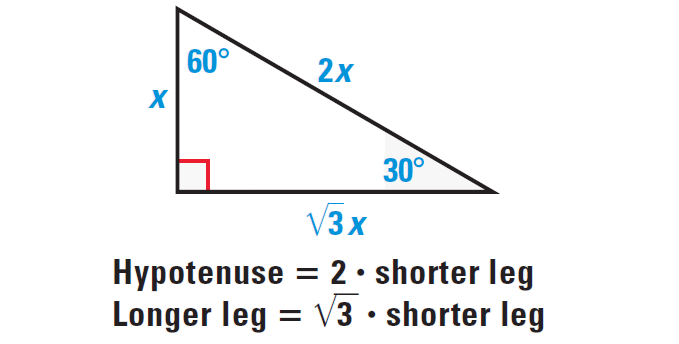
Special Right Triangles

Kutasoftware Geometry Special Right Triangles Part 2 Youtube

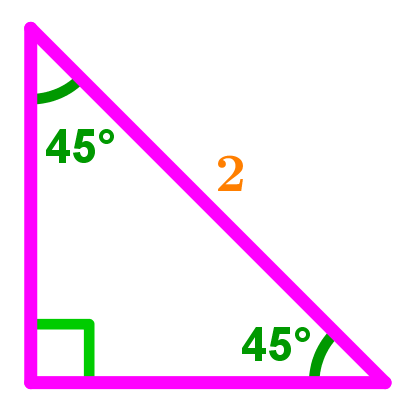
How To Use The Special Right Triangle 45 45 90 Studypug

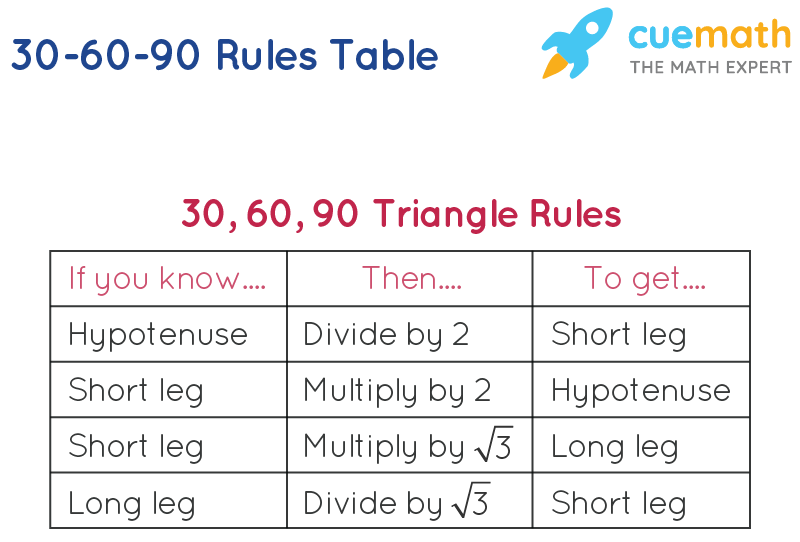
30 60 90 Formula Learn Formula For Calculating The 30 60 90 Measures

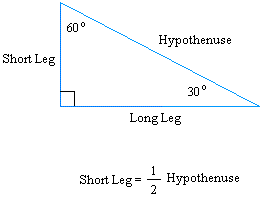
Special Right Triangles

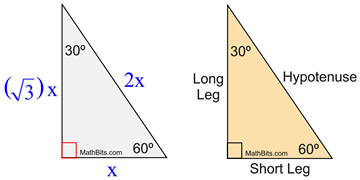
Special Right Triangle 30 60 90 Mathbitsnotebook Geo Ccss Math

The Complete Guide To The 30 60 90 Triangle

30 60 90 Special Right Triangle Calculator Inch Calculator

1

The 30 60 90 Triangle Topics In Trigonometry

1

Special Right Triangles Activity Builder By Desmos

30 60 90 Right Triangles Solutions Examples Videos

21 Images 30 60 90 Right Triangle

The Complete Guide To The 30 60 90 Triangle

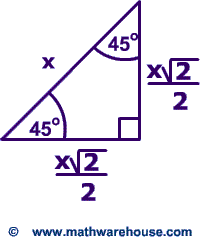
Special Right Triangles Formulas 30 60 90 And 45 45 90 Special Right Triangles Examples Pictures And Practice Problems

30 60 90 Triangle Rules

30 60 90 And 45 45 90 Triangle Calculator

30 60 90 Triangle Theorem Ratio Formula Video

Geometry 8 4 Special Right Triangles This Is

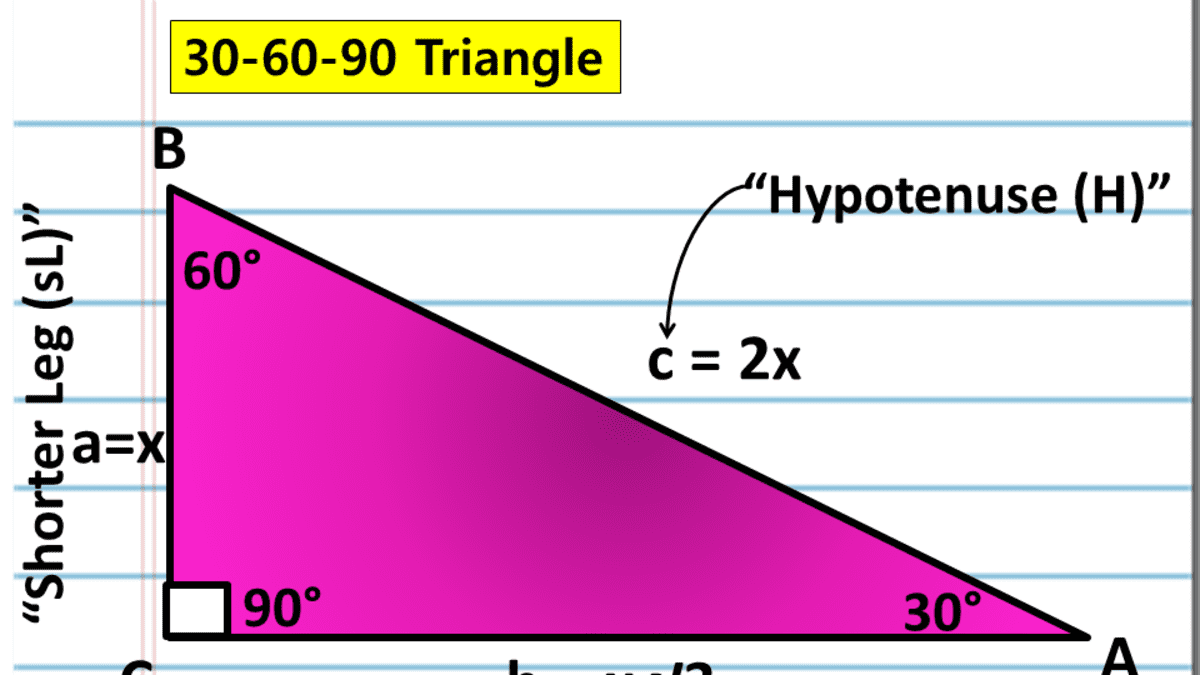
A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation

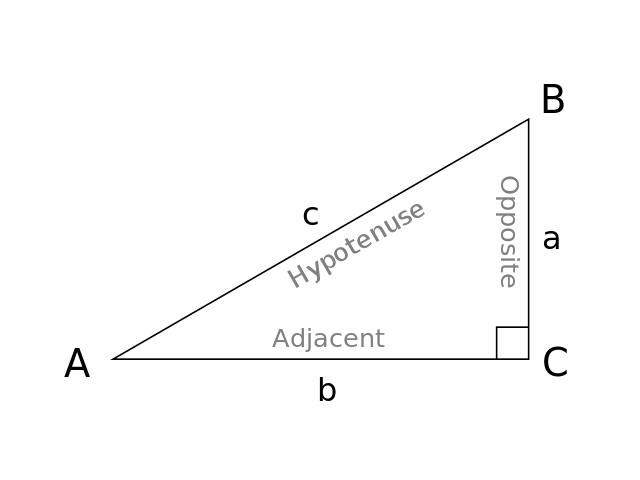
30 60 90 Triangle Formulas Rules And Sides Science Trends

A Quick Guide To The 30 60 90 Degree Triangle Dummies

Rcsdk12 Org

Special Right Triangles Part 1 45 45 90 And 30 60 90 Youtube

30 60 90 Triangle Explanation Examples

30 60 90 Triangle Calculator Formula Rules

Solve A 30 60 90 Triangle With Gradea

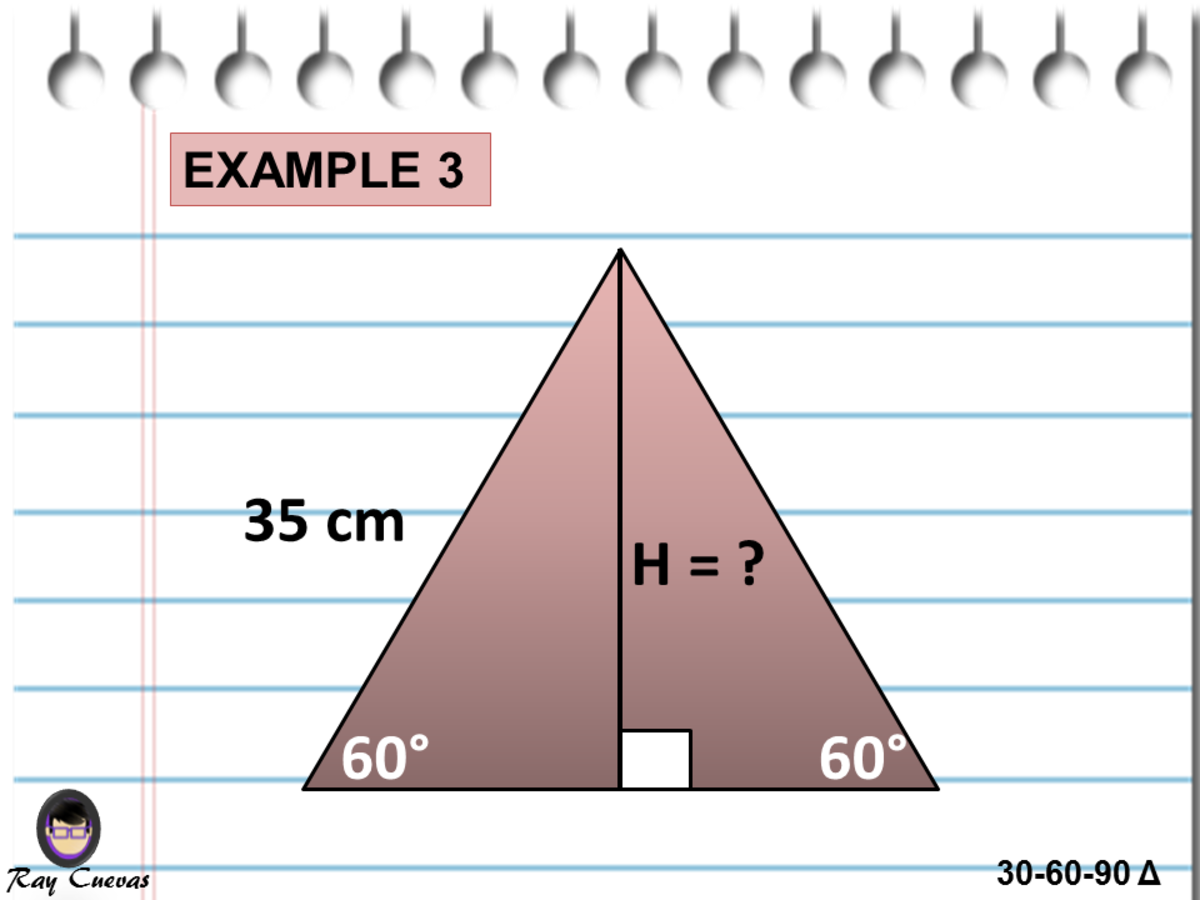
A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation

Right Triangles Gmat Free

How To Work With 30 60 90 And 45 45 90 Degree Triangles Dummies

30 60 90 Triangle Theorem Ratio Formula Video

Incoming Term: special right triangles 30 60 90 formula, special right triangles 30 60 90 calculator, special right triangle 30-60-90 rule, special right triangles calculator 30 60 90 with radicals, how to do special right triangles 30 60 90, how do you solve a 30 60 90 triangle,